Lineer Regrassion

Gerekli Kütüphanelerin Dahil Edilmesi

from sklearn.datasets import load_boston
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.preprocessing import StandardScaler, MinMaxScaler
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression

Veri Setini Yükleme ve Veriyi Tanıma İşlemleri

X,y = load_boston(return_X_y=True)

Boston dataseti 13 girdi 506 örnekten oluşmaktadır. Bostonda emlak fiyatlarının regresyon tahminlerinin yapılması için bölgenin çeşitli özelliklerinin istatistiksel vb. verilerini içermektedir.

print("Features label",X.shape)
print("Targets label",y.shape)

Features label (506, 13)
Targets label (506,)

load_boston().keys()

dict_keys(['data', 'target', 'feature_names', 'DESCR', 'filename', 'data_module'])

13 adet özellik sütununun isimleri aşağıdadır.

print(load_boston().feature_names)

['CRIM' 'ZN' 'INDUS' 'CHAS' 'NOX' 'RM' 'AGE' 'DIS' 'RAD' 'TAX' 'PTRATIO'
 'B' 'LSTAT']

Özellik kolonlarının açıklamalarını ve veri seti hakkındaki bilgileri aşağıdan daha detaylı inceleyebilirsiniz.

print(load_boston().DESCR)

print(load_boston().filename)

boston_house_prices.csv

Boston veri setimizi dataframe olarak tanıtıyoruz

df_boston = pd.DataFrame(X, columns = load_boston().feature_names)

df_boston.head()

CRIM	ZN	INDUS	CHAS	NOX	RM	AGE	DIS	RAD	TAX	PTRATIO	B	LSTAT
0	0.00632	18.0	2.31	0.0	0.538	6.575	65.2	4.0900	1.0	296.0	15.3	396.90
1	0.02731	0.0	7.07	0.0	0.469	6.421	78.9	4.9671	2.0	242.0	17.8	396.90
2	0.02729	0.0	7.07	0.0	0.469	7.185	61.1	4.9671	2.0	242.0	17.8	392.83
3	0.03237	0.0	2.18	0.0	0.458	6.998	45.8	6.0622	3.0	222.0	18.7	394.63
4	0.06905	0.0	2.18	0.0	0.458	7.147	54.2	6.0622	3.0	222.0	18.7	396.90

Veri Ön İşleme İşlemlerine Giriş

Veride Null değerlerin varlığını inceliyoruz.

df_boston.isnull().sum()

CRIM       0
ZN         0
INDUS      0
CHAS       0
NOX        0
RM         0
AGE        0
DIS        0
RAD        0
TAX        0
PTRATIO    0
B          0
LSTAT      0
dtype: int64

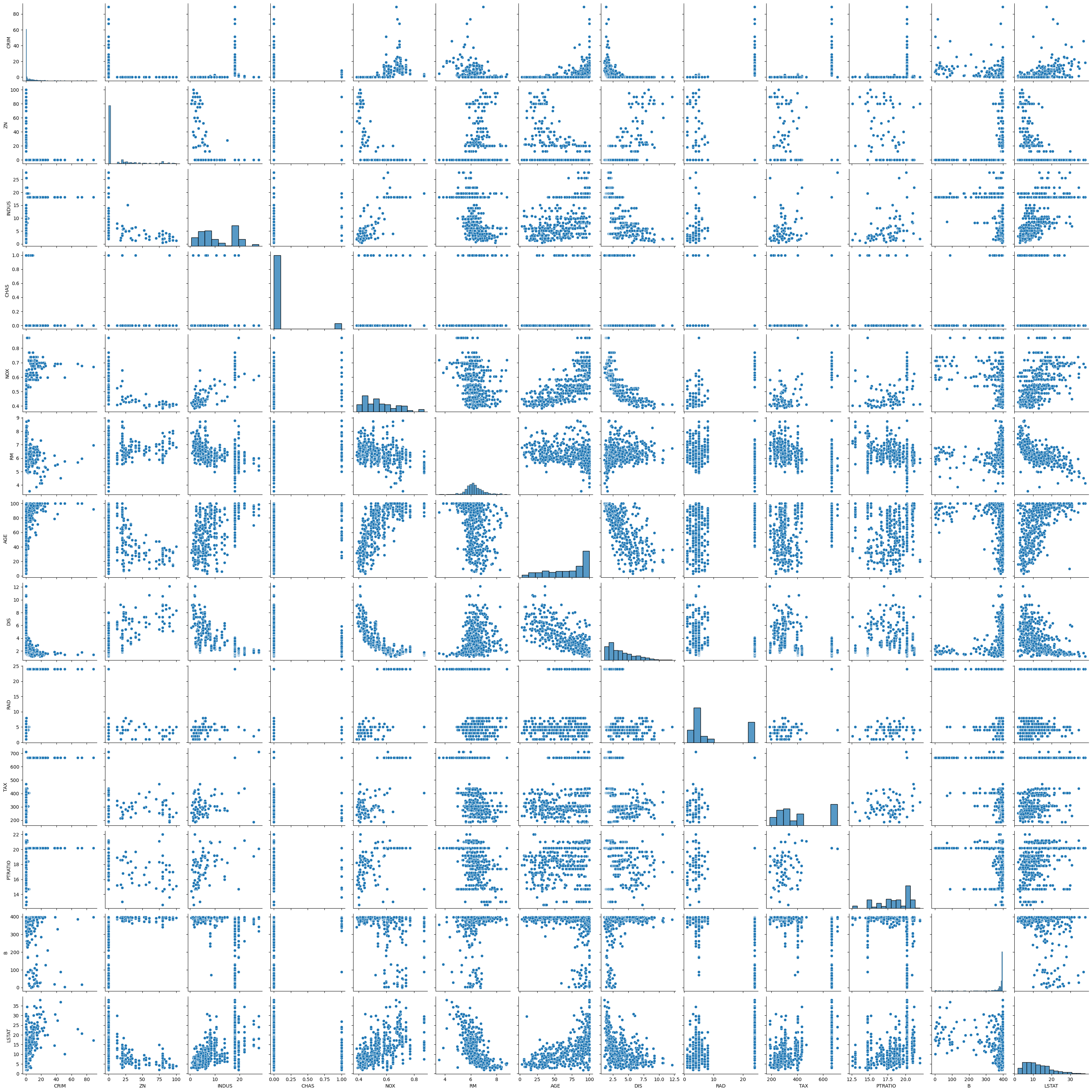
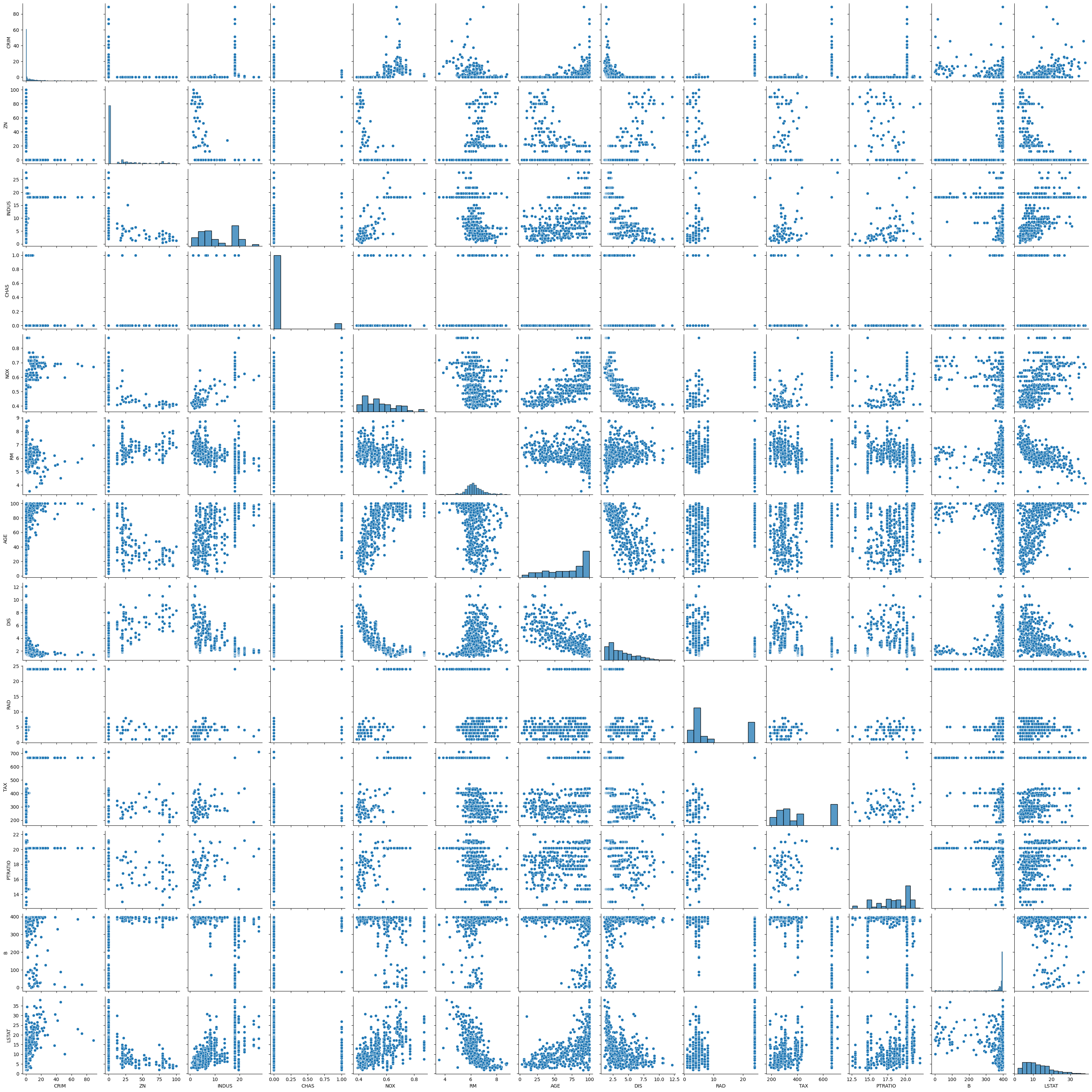
Tüm özellik kolonlarının birbirlerine göre dağılım grafiklerini ve dağılımları inceliyoruz.

sns.pairplot(df_boston)

Featurlar Arasındaki Korelasyon Katsayılarının İncelenmesi ve Göreselleştirilmesi

Veri setimizin ortalama, standart sapması vs. özelliklerini inceliyoruz.

df_boston.describe()

CRIM	ZN	INDUS	CHAS	NOX	RM	AGE	DIS	RAD	TAX	PTRATIO	B	LSTAT
count	506.000000	506.000000	506.000000	506.000000	506.000000	506.000000	506.000000	506.000000	506.000000	506.000000	506.000000	506.000000
mean	3.613524	11.363636	11.136779	0.069170	0.554695	6.284634	68.574901	3.795043	9.549407	408.237154	18.455534	356.674032
std	8.601545	23.322453	6.860353	0.253994	0.115878	0.702617	28.148861	2.105710	8.707259	168.537116	2.164946	91.294864
min	0.006320	0.000000	0.460000	0.000000	0.385000	3.561000	2.900000	1.129600	1.000000	187.000000	12.600000	0.320000
25%	0.082045	0.000000	5.190000	0.000000	0.449000	5.885500	45.025000	2.100175	4.000000	279.000000	17.400000	375.377500
50%	0.256510	0.000000	9.690000	0.000000	0.538000	6.208500	77.500000	3.207450	5.000000	330.000000	19.050000	391.440000
75%	3.677083	12.500000	18.100000	0.000000	0.624000	6.623500	94.075000	5.188425	24.000000	666.000000	20.200000	396.225000
max	88.976200	100.000000	27.740000	1.000000	0.871000	8.780000	100.000000	12.126500	24.000000	711.000000	22.000000	396.900000

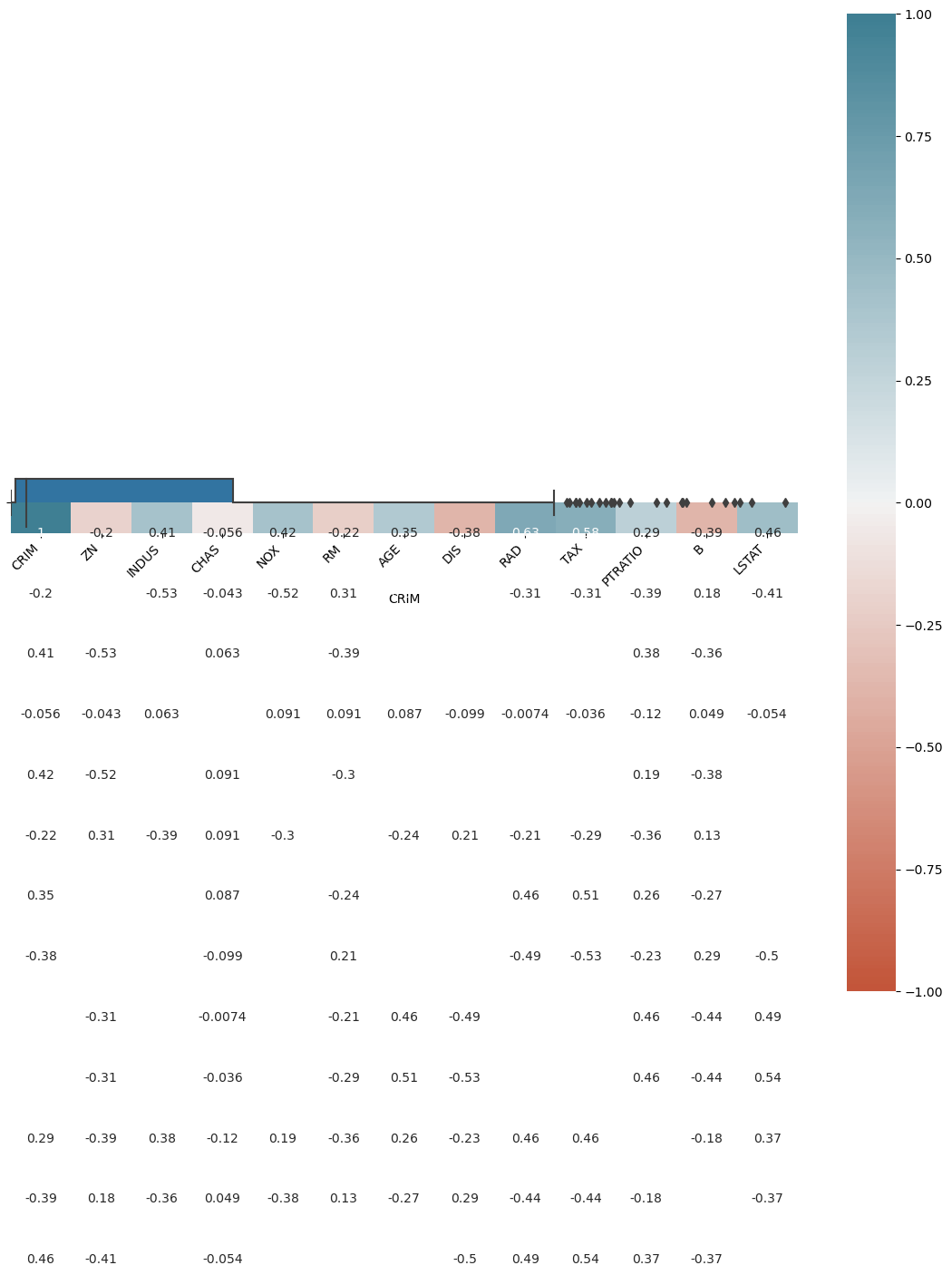
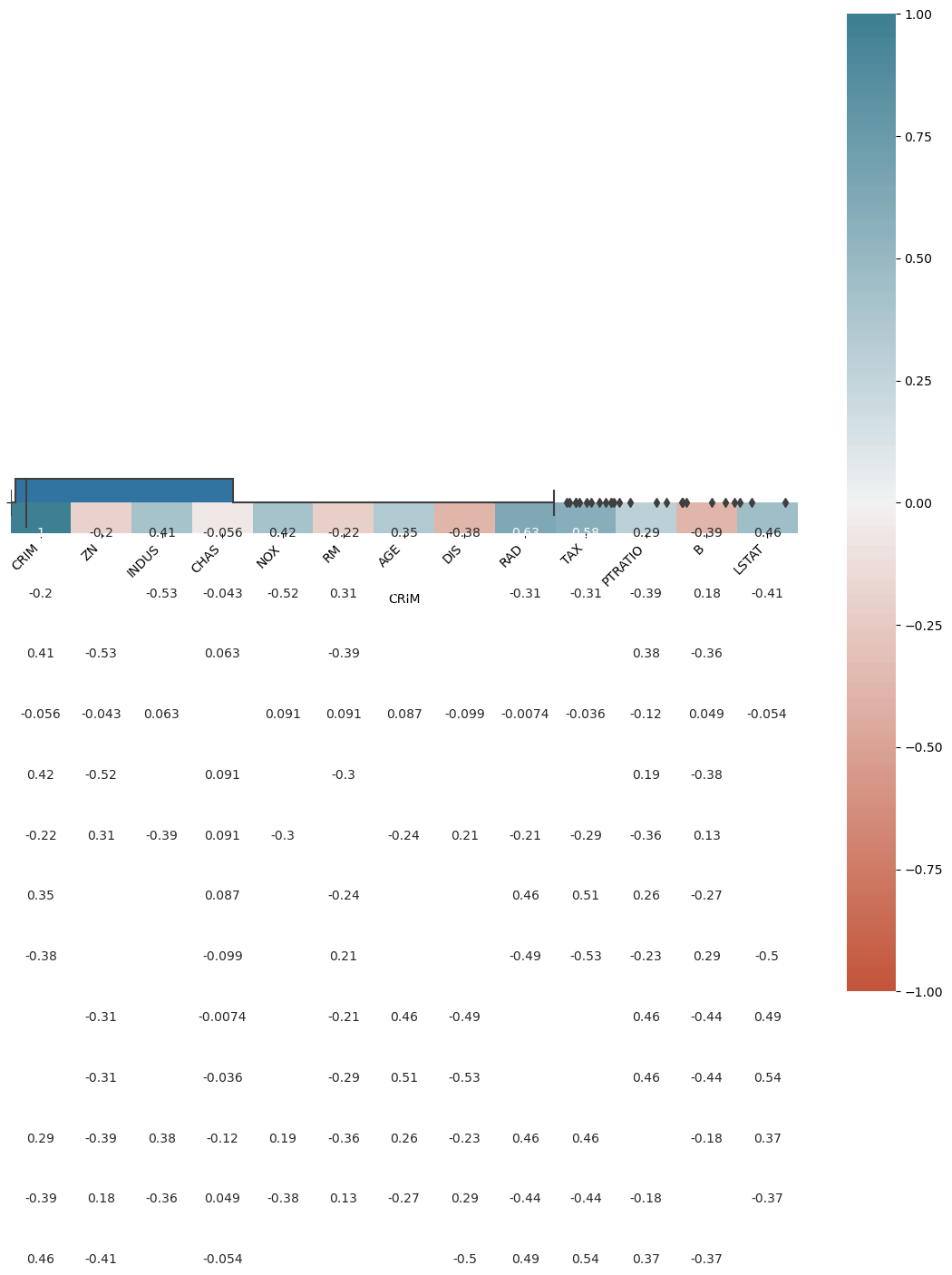
Özellik sütunlarının birbirleri arasındaki korelasyon katsayıları.

df_boston.corr()

CRIM	ZN	INDUS	CHAS	NOX	RM	AGE	DIS	RAD	TAX	PTRATIO	B	LSTAT
CRIM	1.000000	-0.200469	0.406583	-0.055892	0.420972	-0.219247	0.352734	-0.379670	0.625505	0.582764	0.289946	-0.385064
ZN	-0.200469	1.000000	-0.533828	-0.042697	-0.516604	0.311991	-0.569537	0.664408	-0.311948	-0.314563	-0.391679	0.175520
INDUS	0.406583	-0.533828	1.000000	0.062938	0.763651	-0.391676	0.644779	-0.708027	0.595129	0.720760	0.383248	-0.356977
CHAS	-0.055892	-0.042697	0.062938	1.000000	0.091203	0.091251	0.086518	-0.099176	-0.007368	-0.035587	-0.121515	0.048788
NOX	0.420972	-0.516604	0.763651	0.091203	1.000000	-0.302188	0.731470	-0.769230	0.611441	0.668023	0.188933	-0.380051
RM	-0.219247	0.311991	-0.391676	0.091251	-0.302188	1.000000	-0.240265	0.205246	-0.209847	-0.292048	-0.355501	0.128069
AGE	0.352734	-0.569537	0.644779	0.086518	0.731470	-0.240265	1.000000	-0.747881	0.456022	0.506456	0.261515	-0.273534
DIS	-0.379670	0.664408	-0.708027	-0.099176	-0.769230	0.205246	-0.747881	1.000000	-0.494588	-0.534432	-0.232471	0.291512
RAD	0.625505	-0.311948	0.595129	-0.007368	0.611441	-0.209847	0.456022	-0.494588	1.000000	0.910228	0.464741	-0.444413
TAX	0.582764	-0.314563	0.720760	-0.035587	0.668023	-0.292048	0.506456	-0.534432	0.910228	1.000000	0.460853	-0.441808
PTRATIO	0.289946	-0.391679	0.383248	-0.121515	0.188933	-0.355501	0.261515	-0.232471	0.464741	0.460853	1.000000	-0.177383
B	-0.385064	0.175520	-0.356977	0.048788	-0.380051	0.128069	-0.273534	0.291512	-0.444413	-0.441808	-0.177383	1.000000
LSTAT	0.455621	-0.412995	0.603800	-0.053929	0.590879	-0.613808	0.602339	-0.496996	0.488676	0.543993	0.374044	-0.366087

Korelasyon katsayılarının görselleştirilmesi.

corr = df_boston.corr()

plt.figure(figsize=(14, 14))
ax = sns.heatmap(
    corr, 
    vmin=-1, vmax=1, center=0,
    cmap=sns.diverging_palette(20, 220, n=200),
    square=True, annot = True
)
ax.set_xticklabels(
    ax.get_xticklabels(),
    rotation=45,
    horizontalalignment='right'
)
ax.set_ylim(len(corr)+0.5, -0.5);

Veride Aykırı Değerlerin(Outliers) Varlığının İncelenmesi ve Yok Edilmesi Adımları

Öncelikle outlier değerlerini daha iyi anlayabilmek için "CRIM" sütnunun kutu dağılımını inceleyerek outliers değerleri gözlemliyoruz.

df_crım = df_boston["CRIM"].copy()

print(df_crım)

0      0.00632
1      0.02731
2      0.02729
3      0.03237
4      0.06905
        ...   
501    0.06263
502    0.04527
503    0.06076
504    0.10959
505    0.04741
Name: CRIM, Length: 506, dtype: float64

sns.boxplot(x=df_boston["CRIM"])

AxesSubplot:xlabel='CRIM'

Veride Outliers satırlarını çıkartırken "CHAS" sütunundaki değerler hesaba katılmamıştır.Çünkü "CHAS" sütunu 0 ve 1 değerlerinden oluştuğu için tüm 1 değerleri outlier olarak belirlenecek ve veri setinden silinecektir. Bunu önlemek için böyle bir önlem alınmıştır !!!!!

k = 0
for i in range(len(df_boston["CHAS"])):
    a = int(df_boston["CHAS"][i])
    if a == 1:
        k += 1
print("Nehre Kıyısı Olan Ev Sayısı",k)

Nehre Kıyısı Olan Ev Sayısı 35

Outliers değer olan satırları veriden silmek için veri setindeki elemanların z skorlarını alıyoruz. Z skoru bir degerin normal dagilimda gerceklesme olasiligini bulmamizi saglar. Z skoru |3| değerinden büyük ise o veri outlier bir veridir.

#Outlier detection with Z-Score
from scipy import stats
import numpy as np

df_boston1 = df_boston.drop(columns = ["CHAS"])
z_score = np.abs(stats.zscore(df_boston1))
print(z_score)
print(len(z_score))

Outlier verileri veri setimizden siliyoruz.

outliers = list(set(np.where(z_score > 3)[0]))
new_df = df_boston.drop(outliers,axis = 0).reset_index(drop = False)
display(new_df)

y_new = y[list(new_df["index"])]
len(y_new)

index	CRIM	ZN	INDUS	CHAS	NOX	RM	AGE	DIS	RAD	TAX	PTRATIO	B	LSTAT
0	0	0.00632	18.0	2.31	0.0	0.538	6.575	65.2	4.0900	1.0	296.0	15.3	396.90
1	1	0.02731	0.0	7.07	0.0	0.469	6.421	78.9	4.9671	2.0	242.0	17.8	396.90
2	2	0.02729	0.0	7.07	0.0	0.469	7.185	61.1	4.9671	2.0	242.0	17.8	392.83
3	3	0.03237	0.0	2.18	0.0	0.458	6.998	45.8	6.0622	3.0	222.0	18.7	394.63
4	4	0.06905	0.0	2.18	0.0	0.458	7.147	54.2	6.0622	3.0	222.0	18.7	396.90
...	...	...	...	...	...	...	...	...	...	...	...	...	...
443	501	0.06263	0.0	11.93	0.0	0.573	6.593	69.1	2.4786	1.0	273.0	21.0	391.99
444	502	0.04527	0.0	11.93	0.0	0.573	6.120	76.7	2.2875	1.0	273.0	21.0	396.90
445	503	0.06076	0.0	11.93	0.0	0.573	6.976	91.0	2.1675	1.0	273.0	21.0	396.90
446	504	0.10959	0.0	11.93	0.0	0.573	6.794	89.3	2.3889	1.0	273.0	21.0	393.45
447	505	0.04741	0.0	11.93	0.0	0.573	6.030	80.8	2.5050	1.0	273.0	21.0	396.90

448

X_new = new_df.drop('index', axis = 1)

X_new.describe()

CRIM	ZN	INDUS	CHAS	NOX	RM	AGE	DIS	RAD	TAX	PTRATIO	B	LSTAT
count	448.000000	448.000000	448.000000	448.000000	448.000000	448.000000	448.000000	448.000000	448.000000	448.000000	448.000000	448.000000
mean	2.408685	9.296875	10.982545	0.073661	0.550727	6.277942	68.235045	3.788160	8.716518	393.089286	18.398661	374.135089
std	4.764060	19.261826	6.740875	0.261510	0.113707	0.624083	27.738769	1.930332	8.171676	160.901935	2.138179	51.762313
min	0.006320	0.000000	0.460000	0.000000	0.385000	4.368000	2.900000	1.129600	1.000000	188.000000	12.600000	83.450000
25%	0.082598	0.000000	5.190000	0.000000	0.453000	5.887750	45.675000	2.181375	4.000000	277.000000	17.300000	377.677500
50%	0.224635	0.000000	8.560000	0.000000	0.528000	6.194000	75.500000	3.366650	5.000000	311.000000	18.700000	392.215000
75%	2.176878	12.500000	18.100000	0.000000	0.614000	6.590750	93.800000	5.116700	8.000000	437.000000	20.200000	396.900000
max	28.655800	80.000000	27.740000	1.000000	0.871000	8.375000	100.000000	9.222900	24.000000	711.000000	21.200000	396.900000

Yeni veri setimizin matrissel boyutu (448,13) olmuştur. İlk veri seti (506,13) olduğu göz önüne alınarak 58 veri satırı outliers olarak tespit edilip veriden silinmiştir.

print(len(y_new))
print(X_new.shape)

448
(448, 13)

X_new.info()

Linear Regresion Modellerinin Oluşturulması

1) Normalize Edilmiş ve Outliers uygulanmış girdiler ile oluşturulmuş model:

X_scl = StandardScaler().fit_transform(X_new)

X_train, X_test, y_train, y_test = train_test_split(X_scl,y_new, test_size=0.3, random_state=42)

model = LinearRegression()
model.fit(X_train,y_train)

LinearRegression()

print("Train set doğruluk skoru",model.score(X_train,y_train))
print("Test set doğruluk skoru",model.score(X_test,y_test))

Train set doğruluk skoru 0.7300275738890303
Test set doğruluk skoru 0.7262644595320192

print("Model Linear Regression Denklemi Girdilerin Ağırlık Değerleri:")
print("*****************************"*2)
for i in range(X_new.shape[1]):    
    print("Feature:",X_new.columns[i],"     Coefficent:",model.coef_[i])
print("*****************************"*2)
print("Model Bias Değeri",model.intercept_)

MODEL Denklemi

f(x) = x1.(-0.6232915117704749) + x2.(0.20681549725170598) + x3.(0.4866594709201995) + x4.(0.6094681951041256) + x5.(-1.8854778838035968) + x6.(2.972984539726412) + x7.(-0.24617193422155162) + x8.(-2.483054981411919) + x9.(2.0866963867596273) + x10.(-1.3352511053788594) + x11.(-2.07362742795935) + x12.(0.5507950528783419) + x13.(3.382569850079229) + (23.00316433536967)

y_pred = model.predict(X_test)

for i in range(len(y_pred)):
    print("MODEL GERÇEK DEĞERİ:",y_test[i],
          "***"*2,
          "MODEL PREDİCTİON DEĞERİ:",y_pred[i])

Test veri setindeki ilk satır değeri modelde belirlenen ağırlık ve bias değerleri ile çarpılarak tahmin işlemi yapılmıştır. predict() metodu ile tüm test verimizin tahmin değerleri oluşturulabilir. Aşağıda sadece predict() metodunun işleyişi anlaşılması için matamatiksel işlemi yapılmıştır. Diğer modellerde de aynı şekilde bu işlem tekrar edilmiştir. Bu açıklama satırı tüm modeller için tek tek yazılmayacaktır.

ağırlık1 = 0
ağırlıklar = 0
for i in range(13):
    ağırlıklar = X_test[0][i] * model.coef_[i]
    ağırlık1 +=  ağırlıklar
predict1 = ağırlık1 + model.intercept_
print("Tahmin edilen değer",predict1)
print("Gerçek değer",y_test[0])

Tahmin edilen değer 28.571848105506398
Gerçek değer 26.4

a = np.arange(-6,6,0.089)
b = np.arange(0,135)

plt.figure(figsize=(18,9))
plt.suptitle("MODEL TAHMİN GRAFİĞİ DENKLEMİNİN ÇİZDİRİLMESİ")

plt.subplot(1,3,1)
plt.plot(a,y_pred,"r")
plt.plot(X_test,y_pred,'o')
plt.plot(a,y_pred)
plt.legend(df_boston.columns)
plt.tight_layout()
plt.title("Tahminleme değerleri Grafiği")

plt.subplot(1,3,2)
plt.plot(a,y_pred,"r")
plt.plot(X_test,y_test,'o')
plt.legend(df_boston.columns)
plt.tight_layout()
plt.title("Gerçek değerler Grafiği")

plt.subplot(1,3,3)
plt.plot(b,y_pred,"b")
plt.title("Model Denklem Grafiği")

plt.show()

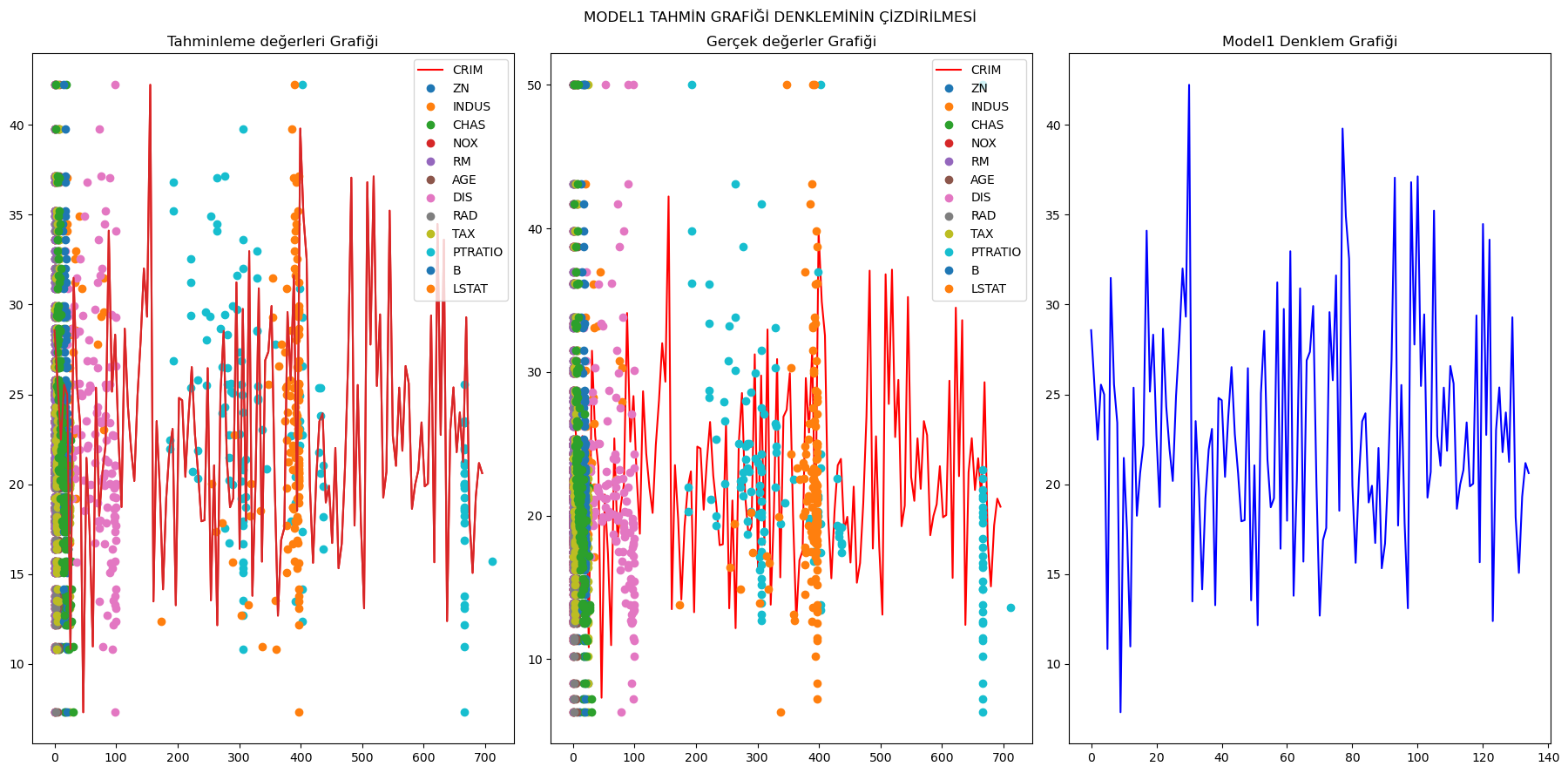
2) Normalize Edilmemiş ama Outliers uygulanmış girdiler ile oluşturulmuş model1:

X_train1, X_test1, y_train1, y_test1 = train_test_split(X_new,y_new, test_size=0.3, random_state=42)

model1 = LinearRegression().fit(X_train1,y_train1)

print("Train set doğruluk skoru",model1.score(X_train1,y_train1))
print("Test set doğruluk skoru",model1.score(X_test1,y_test1))

Train set doğruluk skoru 0.7300275738890302
Test set doğruluk skoru 0.7262644595320187

print("Model1 Linear Regression Denklemi Girdilerin Ağırlık Değerleri:")
print("*****************************"*2)
for i in range(X_new.shape[1]):    
    print("Feature:",X_new.columns[i],"     Coefficent:",model1.coef_[i])
print("*****************************"*2)
print("Model1 Bias Değeri",model1.intercept_)

MODEL1 Denklemi:

f(x) = x1.(-0.13097826393430267) + x2.(0.0107490695698219) + x3.(0.07227600629470217) + x4.(2.3331789133362024) + x5.(-16.60050148737175) + x6.(4.769089026642503) + x7.(-0.008884573675461185) + x8.(-1.2877736450188066) + x9.(0.2556426991343798) + x10.(-0.008307817052884045) + x11.(-0.9708941270421753) + x12.(0.010652746683792933) + x13.(-0.5224434130685673) + (28.244934503472876)

y_pred = model1.predict(X_test1)

for i in range(len(y_pred)):
    print("MODEL1 GERÇEK DEĞERİ:",y_test1[i],
          "***"*2,
          "MODEL1 PREDİCTİON DEĞERİ:",y_pred[i])

ağırlık1 = 0
ağırlıklar = 0
for i in range(13):
    ağırlıklar = X[0][i] * model1.coef_[i]
    ağırlık1 +=  ağırlıklar

predict1 = ağırlık1 + model1.intercept_
print("Tahmin edilen değer",predict1)
print("Gerçek değer",y[0])

Tahmin edilen değer 29.752125355295206
Gerçek değer 24.0

a = np.arange(0,700,5.186)
b = np.arange(0,135)

plt.figure(figsize=(18,9))
plt.suptitle("MODEL1 TAHMİN GRAFİĞİ DENKLEMİNİN ÇİZDİRİLMESİ")

plt.subplot(1,3,1)
plt.plot(a,y_pred,"r")
plt.plot(X_test1,y_pred,'o')
plt.plot(a,y_pred)
plt.legend(df_boston.columns)
plt.tight_layout()
plt.title("Tahminleme değerleri Grafiği")

plt.subplot(1,3,2)
plt.plot(a,y_pred,"r")
plt.plot(X_test1,y_test1,'o')
plt.legend(df_boston.columns)
plt.tight_layout()
plt.title("Gerçek değerler Grafiği")

plt.subplot(1,3,3)
plt.plot(b,y_pred,"b")
plt.title("Model1 Denklem Grafiği")

plt.show()

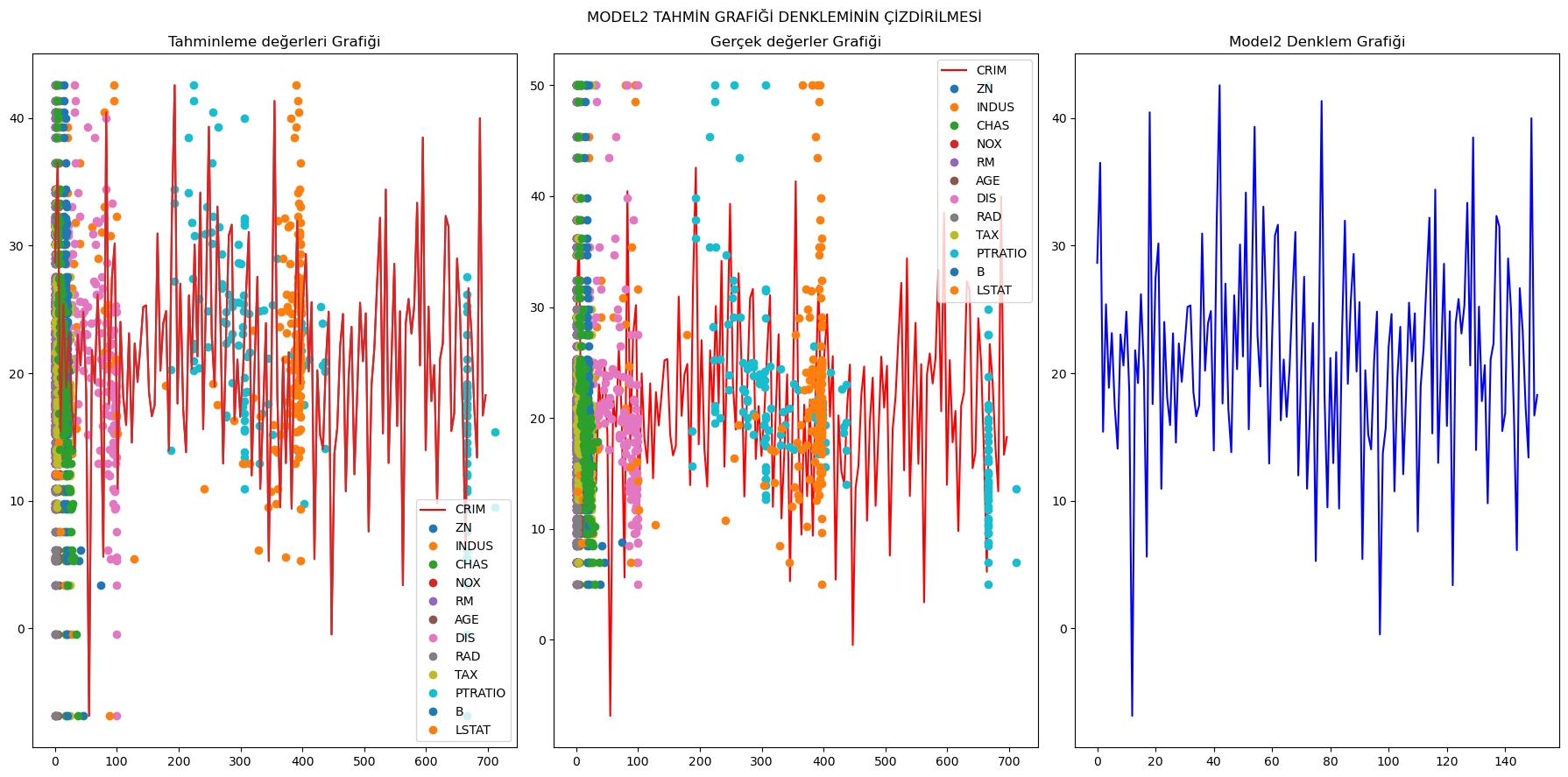
3) Normalize Edilmemiş ve Outliers uygulanmamış girdiler ile oluşturulmuş model2:

X_train2, X_test2, y_train2, y_test2 = train_test_split(X,y, test_size=0.3, random_state=42)

model2 = LinearRegression().fit(X_train2,y_train2)

print("Train set doğruluk skoru",model2.score(X_train2,y_train2))
print("Test set doğruluk skoru",model2.score(X_test2,y_test2))

Train set doğruluk skoru 0.7434997532004697
Test set doğruluk skoru 0.711226005748496

print("Model2 Linear Regression Denklemi Girdilerin Ağırlık Değerleri:")
print("*****************************"*2)
for i in range(df_boston.shape[1]):    
    print("Feature:",df_boston.columns[i],"     Coefficent:",model2.coef_[i])
print("*****************************"*2)
print("Model2 Bias Değeri",model2.intercept_)

MODEL2 Denklemi:

f(x) = x1.(-0.13347010285294425) + x2.(0.03580891359323082) + x3.(0.049522645220057185) + x4.(3.1198351162854077) + x5.(-15.41706089530688) + x6.(4.057199231645392) + x7.(-0.010820835184930837) + x8.(-1.3859982431608768) + x9.(0.24272733982224357) + x10.(-0.00870223436566267) + x11.(-0.9106852081102922) + x12.(0.011794115892570081) + x13.(-0.5471133128239593) + (31.631084035694585)

y_pred = model2.predict(X_test2)

for i in range(len(y_pred)):
    print("MODEL2 GERÇEK DEĞERİ:",y_test2[i],
          "***"*2,
          "MODEL2 PREDİCTİON DEĞERİ:",y_pred[i])

## Test verisindeki ilk değerinin regresyon tahmini ve gerçek değerinin karşılaştırılması
ağırlık1 = 0
ağırlıklar = 0
for i in range(13):
    ağırlıklar = X_test2[0][i] * model2.coef_[i]
    ağırlık1 +=  ağırlıklar
predict1 = ağırlık1 + model2.intercept_
print("Tahmin edilen değer",predict1)
print("Gerçek değer",y_test2[0])

Tahmin edilen değer 28.648960046324085
Gerçek değer 23.6

a = np.arange(0,700,4.61)
b = np.arange(0,152)

plt.figure(figsize=(18,9))
plt.suptitle("MODEL2 TAHMİN GRAFİĞİ DENKLEMİNİN ÇİZDİRİLMESİ")

plt.subplot(1,3,1)
plt.plot(a,y_pred,"r")
plt.plot(X_test2,y_pred,'o')
plt.plot(a,y_pred)
plt.legend("Denklem")
plt.legend(df_boston.columns)
plt.tight_layout()
plt.title("Tahminleme değerleri Grafiği")

plt.subplot(1,3,2)
plt.plot(a,y_pred,"r")
plt.plot(X_test2,y_test2,'o')
plt.legend(df_boston.columns)
plt.tight_layout()
plt.title("Gerçek değerler Grafiği")

plt.subplot(1,3,3)
plt.plot(b,y_pred,"b")
plt.title("Model2 Denklem Grafiği")

plt.show()

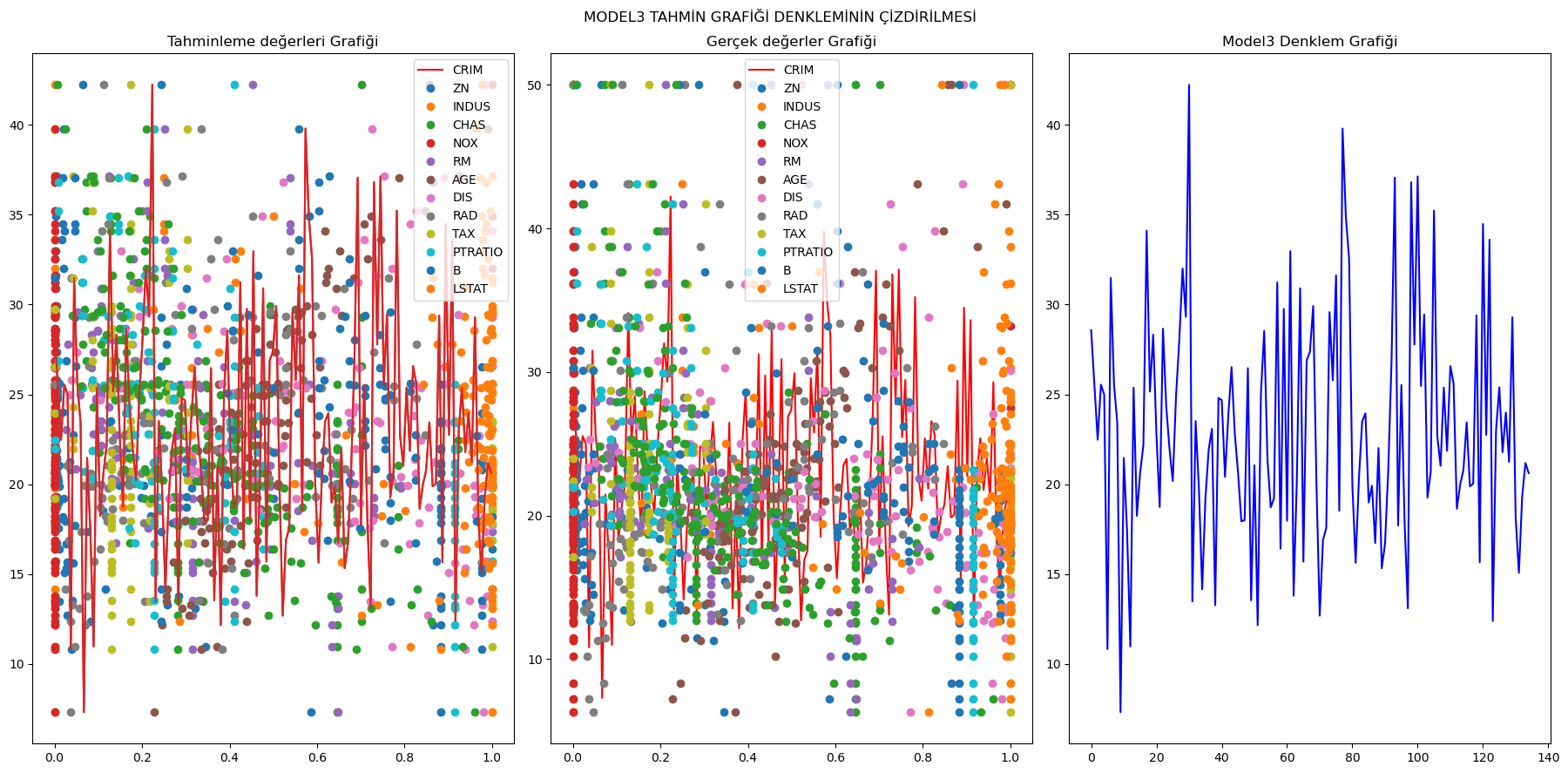
4) Outliers uygulanmış ve MinMax Scaller uygulanmış model3:

X_minmax= MinMaxScaler().fit_transform(X_new)

X_train3, X_test3, y_train3, y_test3 = train_test_split(X_minmax,y_new, test_size=0.3, random_state=42)

model3 = LinearRegression().fit(X_train3,y_train3)

print("Train set doğruluk skoru",model3.score(X_train3,y_train3))
print("Test set doğruluk skoru",model3.score(X_test3,y_test3))

Train set doğruluk skoru 0.7300275738890303
Test set doğruluk skoru 0.7262644595320192

print("Model3 Linear Regression Denklemi Girdilerin Ağırlık Değerleri:")
print("*****************************"*2)
for i in range(X_new.shape[1]):    
    print("Feature:",X_new.columns[i],"     Coefficent:",model3.coef_[i])
print("*****************************"*2)
print("Model3 Bias Değeri",model3.intercept_)

MODEL3 Denklemi:

f(x) = x1.(-3.752459153020569) + x2.(0.8599255655852653) + x3.(1.971689451719393) + x4.(2.333178913336127) + x5.(-8.067843722862678) + x6.(19.109739729756456) + x7.(-0.8626921038876417) + x8.(-10.42233844123072) + x9.(5.879782080090829) + x10.(-4.344988318658385) + x11.(-8.349689492562684) + x12.(3.339103448034986) + x13.(-15.809137679454942) + (27.68275880501959)

y_pred = model3.predict(X_test3)

for i in range(len(y_pred)):
    print("MODEL3 GERÇEK DEĞERİ:",y_test3[i],
          "***"*2,
          "MODEL3 PREDİCTİON DEĞERİ:",y_pred[i])

## Test verisindeki ilk değerinin regresyon tahmini ve gerçek değerinin karşılaştırılması
ağırlık1 = 0
ağırlıklar = 0
for i in range(13):
    ağırlıklar = X_test3[0][i] * model3.coef_[i]
    ağırlık1 +=  ağırlıklar
predict1 = ağırlık1 + model3.intercept_
print("Tahmin edilen değer",predict1)
print("Gerçek değer",y_test3[0])

Tahmin edilen değer 28.57184810550641
Gerçek değer 26.4

a = np.arange(0,1,0.00745)
b = np.arange(0,135)

plt.figure(figsize=(18,9))
plt.suptitle("MODEL3 TAHMİN GRAFİĞİ DENKLEMİNİN ÇİZDİRİLMESİ")

plt.subplot(1,3,1)
plt.plot(a,y_pred,"r")
plt.plot(X_test3,y_pred,'o')
plt.plot(a,y_pred)
plt.legend(df_boston.columns)
plt.tight_layout()
plt.title("Tahminleme değerleri Grafiği")

plt.subplot(1,3,2)
plt.plot(a,y_pred,"r")
plt.plot(X_test3,y_test3,'o')
plt.legend(df_boston.columns)
plt.tight_layout()
plt.title("Gerçek değerler Grafiği")

plt.subplot(1,3,3)
plt.plot(b,y_pred,"b")
plt.title("Model3 Denklem Grafiği")

plt.show()

Oluşturulan tüm modellerin train ve test doğruluk skorları aşağıda yazdırılmıştır. En yüksek train doğruluğunu model2 yakalasa da test doğruluğu olarak diğer modellerden geride kalmıştır. Model, model1 ve model3 train ve test doğrulukları birbirlerine eşittir.

print("MODEL Train set doğruluk skoru",model.score(X_train,y_train))
print("MODEL Test set doğruluk skoru",model.score(X_test,y_test))
print("***"*17)
print("MODEL1 Train set doğruluk skoru",model1.score(X_train1,y_train1))
print("MODEL1 Test set doğruluk skoru",model1.score(X_test1,y_test1))
print("***"*17)
print("MODEL2 Train set doğruluk skoru",model2.score(X_train2,y_train2))
print("MODEL2 Test set doğruluk skoru",model2.score(X_test2,y_test2))
print("***"*17)
print("MODEL3 Train set doğruluk skoru",model3.score(X_train3,y_train3))
print("MODEL3 Test set doğruluk skoru",model3.score(X_test3,y_test3))

Poly Lineer Regression

from sklearn.datasets import load_boston
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.preprocessing import StandardScaler, MinMaxScaler
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression

X,y = load_boston(return_X_y=True)

print("Features label",X.shape)
print("Targets label",y.shape)

Features label (506, 13)
Targets label (506,)

load_boston().keys()

dict_keys(['data', 'target', 'feature_names', 'DESCR', 'filename', 'data_module'])

print(load_boston().feature_names)

['CRIM' 'ZN' 'INDUS' 'CHAS' 'NOX' 'RM' 'AGE' 'DIS' 'RAD' 'TAX' 'PTRATIO'
 'B' 'LSTAT']

print(load_boston().DESCR)

df_boston = pd.DataFrame(X, columns = load_boston().feature_names)

df_boston.head()

CRIM	ZN	INDUS	CHAS	NOX	RM	AGE	DIS	RAD	TAX	PTRATIO	B	LSTAT
0	0.00632	18.0	2.31	0.0	0.538	6.575	65.2	4.0900	1.0	296.0	15.3	396.90
1	0.02731	0.0	7.07	0.0	0.469	6.421	78.9	4.9671	2.0	242.0	17.8	396.90
2	0.02729	0.0	7.07	0.0	0.469	7.185	61.1	4.9671	2.0	242.0	17.8	392.83
3	0.03237	0.0	2.18	0.0	0.458	6.998	45.8	6.0622	3.0	222.0	18.7	394.63
4	0.06905	0.0	2.18	0.0	0.458	7.147	54.2	6.0622	3.0	222.0	18.7	396.90

df_boston.isnull().sum()

CRIM       0
ZN         0
INDUS      0
CHAS       0
NOX        0
RM         0
AGE        0
DIS        0
RAD        0
TAX        0
PTRATIO    0
B          0
LSTAT      0
dtype: int64

df_boston.describe()

CRIM	ZN	INDUS	CHAS	NOX	RM	AGE	DIS	RAD	TAX	PTRATIO	B	LSTAT
count	506.000000	506.000000	506.000000	506.000000	506.000000	506.000000	506.000000	506.000000	506.000000	506.000000	506.000000	506.000000
mean	3.613524	11.363636	11.136779	0.069170	0.554695	6.284634	68.574901	3.795043	9.549407	408.237154	18.455534	356.674032
std	8.601545	23.322453	6.860353	0.253994	0.115878	0.702617	28.148861	2.105710	8.707259	168.537116	2.164946	91.294864
min	0.006320	0.000000	0.460000	0.000000	0.385000	3.561000	2.900000	1.129600	1.000000	187.000000	12.600000	0.320000
25%	0.082045	0.000000	5.190000	0.000000	0.449000	5.885500	45.025000	2.100175	4.000000	279.000000	17.400000	375.377500
50%	0.256510	0.000000	9.690000	0.000000	0.538000	6.208500	77.500000	3.207450	5.000000	330.000000	19.050000	391.440000
75%	3.677083	12.500000	18.100000	0.000000	0.624000	6.623500	94.075000	5.188425	24.000000	666.000000	20.200000	396.225000
max	88.976200	100.000000	27.740000	1.000000	0.871000	8.780000	100.000000	12.126500	24.000000	711.000000	22.000000	396.900000

#Outlier detection with Z-Score
from scipy import stats
import numpy as np

df_boston1 = df_boston.drop(columns = ["CHAS"])
z_score = np.abs(stats.zscore(df_boston1))
print(z_score)
print(len(z_score))

         CRIM        ZN     INDUS       NOX        RM       AGE       DIS  \
0    0.419782  0.284830  1.287909  0.144217  0.413672  0.120013  0.140214   
1    0.417339  0.487722  0.593381  0.740262  0.194274  0.367166  0.557160   
2    0.417342  0.487722  0.593381  0.740262  1.282714  0.265812  0.557160   
3    0.416750  0.487722  1.306878  0.835284  1.016303  0.809889  1.077737   
4    0.412482  0.487722  1.306878  0.835284  1.228577  0.511180  1.077737   
..        ...       ...       ...       ...       ...       ...       ...   
501  0.413229  0.487722  0.115738  0.158124  0.439316  0.018673  0.625796   
502  0.415249  0.487722  0.115738  0.158124  0.234548  0.288933  0.716639   
503  0.413447  0.487722  0.115738  0.158124  0.984960  0.797449  0.773684   
504  0.407764  0.487722  0.115738  0.158124  0.725672  0.736996  0.668437   
505  0.415000  0.487722  0.115738  0.158124  0.362767  0.434732  0.613246   

          RAD       TAX   PTRATIO         B     LSTAT  
0    0.982843  0.666608  1.459000  0.441052  1.075562  
1    0.867883  0.987329  0.303094  0.441052  0.492439  
2    0.867883  0.987329  0.303094  0.396427  1.208727  
3    0.752922  1.106115  0.113032  0.416163  1.361517  
4    0.752922  1.106115  0.113032  0.441052  1.026501  
..        ...       ...       ...       ...       ...  
501  0.982843  0.803212  1.176466  0.387217  0.418147  
502  0.982843  0.803212  1.176466  0.441052  0.500850  
503  0.982843  0.803212  1.176466  0.441052  0.983048  
504  0.982843  0.803212  1.176466  0.403225  0.865302  
505  0.982843  0.803212  1.176466  0.441052  0.669058  

[506 rows x 12 columns]
506

y = np.array(y)
y.shape

(506,)

outliers = list(set(np.where(z_score > 3)[0]))
X_new = df_boston.drop(outliers,axis = 0).reset_index(drop = True)
display(new_df)
y_new = np.delete(y,outliers)

CRIM	ZN	INDUS	CHAS	NOX	RM	AGE	DIS	RAD	TAX	PTRATIO	B	LSTAT
0	0.00632	18.0	2.31	0.0	0.538	6.575	65.2	4.0900	1.0	296.0	15.3	396.90
1	0.02731	0.0	7.07	0.0	0.469	6.421	78.9	4.9671	2.0	242.0	17.8	396.90
2	0.02729	0.0	7.07	0.0	0.469	7.185	61.1	4.9671	2.0	242.0	17.8	392.83
3	0.03237	0.0	2.18	0.0	0.458	6.998	45.8	6.0622	3.0	222.0	18.7	394.63
4	0.06905	0.0	2.18	0.0	0.458	7.147	54.2	6.0622	3.0	222.0	18.7	396.90
...	...	...	...	...	...	...	...	...	...	...	...	...
443	0.06263	0.0	11.93	0.0	0.573	6.593	69.1	2.4786	1.0	273.0	21.0	391.99
444	0.04527	0.0	11.93	0.0	0.573	6.120	76.7	2.2875	1.0	273.0	21.0	396.90
445	0.06076	0.0	11.93	0.0	0.573	6.976	91.0	2.1675	1.0	273.0	21.0	396.90
446	0.10959	0.0	11.93	0.0	0.573	6.794	89.3	2.3889	1.0	273.0	21.0	393.45
447	0.04741	0.0	11.93	0.0	0.573	6.030	80.8	2.5050	1.0	273.0	21.0	396.90

X_new.shape

(448, 13)

y_new.shape

(448,)

X_new.info()

class 'pandas.core.frame.DataFrame'
RangeIndex: 448 entries, 0 to 447
Data columns (total 13 columns):
 #   Column   Non-Null Count  Dtype  
---  ------   --------------  -----  
 0   CRIM     448 non-null    float64
 1   ZN       448 non-null    float64
 2   INDUS    448 non-null    float64
 3   CHAS     448 non-null    float64
 4   NOX      448 non-null    float64
 5   RM       448 non-null    float64
 6   AGE      448 non-null    float64
 7   DIS      448 non-null    float64
 8   RAD      448 non-null    float64
 9   TAX      448 non-null    float64
 10  PTRATIO  448 non-null    float64
 11  B        448 non-null    float64
 12  LSTAT    448 non-null    float64
dtypes: float64(13)
memory usage: 45.6 KB

# Veri ön işleme
from sklearn.preprocessing import StandardScaler
X_scl = StandardScaler().fit_transform(X_new)  # Veriyi standartlaştırma

Bu kod bloğunda, X_new değişkeninde bulunan veriler StandardScaler kullanılarak standartlaştırılıyor. Standartlaştırma işlemi, veri setindeki özniteliklerin ortalamasını 0 ve standart sapmasını 1 olacak şekilde ayarlar.

# Polinom özellikleri ekleyerek veri setini genişletme
from sklearn.preprocessing import PolynomialFeatures
poly_features = PolynomialFeatures(degree=1)  # Polinom derecesi belirleniyor
X_poly = poly_features.fit_transform(X_scl)  # Polinom özellikleri ekleniyor

Bu kod bloğunda, PolynomialFeatures kullanılarak, veri setine polinom özellikleri eklenir. Bu, modelin karmaşıklığını ve kapasitesini artırarak daha karmaşık veri yapılarını öğrenmesini sağlar.

# Dönüştürülmüş veri setinin boyutlarını kontrol etme
X_poly.shape

(448, 14)

Bu ifade, polinom özellikleri eklenmiş veri setinin boyutlarını gösterir. Burada 448 satır ve 14 sütun vardır.

# Lineer Regresyon modeli oluşturma ve eğitme
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(X_poly, y_new)  # Modeli polinom özelliklerle eğitme

LinearRegression()

Bu kod bloğunda, LinearRegression modeli oluşturulmuş ve polinom özellikleri içeren veri seti ile eğitilmiştir.

# Başka bir Lineer Regresyon modeli daha oluşturma ve eğitme
model1 = LinearRegression()
model1.fit(X_new, y_new)  # Orijinal veri ile modeli eğitme

LinearRegression()

Bu kod, başka bir lineer regresyon modelini orijinal veri setiyle eğitir. İki modelin karşılaştırılması için bu adım önemlidir.

# Test veri setini belirleme
X_test = X_new  # Test verisi olarak orijinal veriyi kullanma

Test için kullanılacak veri seti, orijinal veri seti X_new olarak belirlenmiştir.

# Test veri setinin boyutunu kontrol etme
X_test.shape

(448, 13)

Bu kod, test veri setinin boyutlarını gösterir. Burada 448 satır ve 13 sütun vardır.

# Test veri setine polinom özellikler eklenmesi
X_test_pred = poly_features.fit_transform(X_test)  # Test verisini dönüştürme

Bu kod bloğu, test veri setine polinom özellikler ekler.

# Dönüştürülmüş test veri setinin boyutlarını kontrol etme
X_test_pred.shape

(448, 14)

Bu ifade, polinom özellikleri eklenmiş test veri setinin boyutlarını gösterir.

# Model kullanarak tahmin yapma
y_pred = model.predict(X_test_pred)  # Polinom modeliyle tahmin yapma

Bu kod bloğu, polinom regresyon modelini kullanarak tahminler yapar.

# Başka bir model kullanarak tahmin yapma
y_pred1 = model1.predict(X_test)  # Lineer modeliyle tahmin yapma

Bu kod, lineer regresyon modeli kullanarak tahminler yapar.

# İlk tahmin değerlerini gösterme
y_pred1[0]  # Lineer modelin ilk tahmini

29.483163224969477

Bu ifade, lineer regresyon modelinin ilk tahmin değerini

gösterir.

y_pred[0]  # Polinom modelin ilk tahmini

-359.57673325992755

Bu ifade, polinom regresyon modelinin ilk tahmin değerini gösterir.

y_new[0]  # Gerçek ilk değer

24.0

Bu kod, veri setindeki ilk gerçek değeri gösterir.

# 'CRIM' özniteliğinin değerlerini gösterme
X_new["CRIM"]  # Orijinal veri setinde 'CRIM' sütunu

0 0.00632
1 0.02731
...
446 0.10959
447 0.04741
Name: CRIM, Length: 448, dtype: float64

Bu kod, CRIM özniteliğinin tüm değerlerini listeler.

X_test["CRIM"]  # Test veri setinde 'CRIM' sütunu

0 0.00632
1 0.02731
...
446 0.10959
447 0.04741
Name: CRIM, Length: 448, dtype: float64

Bu kod, test veri setinde CRIM özniteliğinin tüm değerlerini listeler.

Sonuçların görselleştirilmesi, modelin performansının anlaşılmasında kritik öneme sahiptir. İki farklı görselleştirme yapılarak, polinom ve lineer regresyon modellerinin gerçek verilere ne kadar yakın sonuçlar ürettiği karşılaştırılır.

# Polinom Regresyon sonuçlarını görselleştirme
import matplotlib.pyplot as plt
plt.scatter(np.arange(0, X_new.shape[0]), y_new, color='red', label='Gerçek Veri')
plt.plot(np.arange(0, X_new.shape[0]), y_pred, color='blue', label='Polinom Regresyon')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.show()

Bu kod bloğu, polinom regresyon modelinin sonuçlarını gerçek veriyle birlikte görselleştirir.

# Lineer Regresyon sonuçlarını görselleştirme
plt.scatter(np.arange(0, X_new.shape[0]), y_new, color='red', label='Gerçek Veri')
plt.plot(np.arange(0, X_new.shape[0]), y_pred1, color='blue', label='Lineer Regresyon')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.show()

Bu kod bloğu, lineer regresyon modelinin sonuçlarını gerçek veriyle birlikte görselleştirir.

Son olarak, bir örnek polinom regresyon uygulaması gösterilir. Bu, polinom regresyonun nasıl çalıştığını göstermek için basit bir örnektir.

# Basit bir polinom regresyon örneği
# Kütüphaneleri yükleme
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures

# Örnek veri oluşturma
X = np.array([1, 2, 3, 4, 5]).reshape(-1, 1)  # Giriş verisi
y = np.array([2, 4, 8, 16, 32])  # Çıkış verisi

# Polinom özelliklerini oluşturma
poly_features = PolynomialFeatures(degree=3)
X_poly = poly_features.fit_transform(X)

# Model oluşturma ve eğitme
model = LinearRegression()
model.fit(X_poly, y)

# Tahmin yapma
X_pred = np.linspace(1, 5, 100).reshape(-1, 1)
X_pred_poly = poly_features.transform(X_pred)
y_pred = model.predict(X_pred_poly)

# Sonuçları görselleştirme
plt.scatter(X, y, color='red', label='Gerçek Veri')
plt.plot(X_pred, y_pred, color='blue', label='Polinom Regresyon')
plt.xlabel('X')


plt.ylabel('y')
plt.legend()
plt.show()